Cris’ Image Analysis Blog

The median filter is a non-liner smoothing (blurring) filter where an output pixel is the median value of its neighborhood in the input image. It can be generalized to a percentile filter, where the median is the 50^th percentile.

Noisy “trui” image filtered with a percentile filter, from left to right: 100^th percentile (dilation), 95^th percentile, 75^th percentile, 50^th percentile (median), 25^th percentile, 5^th percentile, 0^th percentile (erosion).

In Mathematical Morphology one talks about a rank filter. Mathematical Morphology is based on the maximum and minimum values of sets (actually the supremum and infimum values, but the difference is just a technicality). For noisy images, it sometimes is advantageous to compute the maximum or minimum ignoring a few values, in fact computing a rank order statistic. So a rank 3 filter is like a maximum filter (a dilation), but ignoring the two largest values in the neighborhood. The equivalence between the rank filter and the percentile filter is obvious.

In this blog post I want to discuss implementations of the median filter (and, by extension, the percentile and rank filters). Because computing the median is a non-linear operation, we cannot use the Fourier transform to aid us. There is also no way to split up the median computation. We can compute the mean of a set by dividing up the set into smaller sets, compute the mean of each subset, then compute the mean of the means. We can do the same for the maximum or minimum computation. But for the median this is not possible. This means that reducing the algorithmic complexity of the median filter is not a trivial exercise.

Naive algorithm

The basic algorithm to compute a median filter would be to compute the median over the neighborhood independently for each output pixel. This is the algorithm implemented in scikit-image (which actually uses the implementation in SciPy’s ndimage), as well as the one in DIPlib up to version 3.3.0 (which is the current release, the next release of DIPlib will include a more efficient algorithm, discussed later).

Computing the median cannot be done in-place. One needs to sort the values, so the simplest approach is to copy them over into a temporary buffer, sort the buffer, and then find the median value. Sorting values takes . We can speed up the process by not sorting the array fully, just enough to get the median value in its place. For example, using the Quicksort algorithm for sorting, we can always skip one of the two sub-arrays. This is called partial sorting, and in C++ is implemented as std::nth_element. Partial sorting has a complexity of on average.

For integer values, sorting complexity is , but there is no reduction in complexity for partial sort in this case.

For a square 2D kernel of pixels, this implementation thus costs per pixel. This is actually a quite efficient algorithm for small kernels, but because of the poor scaling, gets quite expensive for larger ones.

Histogram-based algorithm

Because the median computation cannot be split up, as I mentioned earlier, the only way to reduce the algorithmic complexity of the filter is to somehow update the data in the temporary buffer (remove the pixels exiting the kernel as it is shifted over one pixel, and add the pixels entering), and do so in a manner that makes finding the median cheaper, in a manner that allows re-using the earlier work.

In the case of 8-bit images, sorting can be done efficiently by computing a histogram of the values to be sorted. Finding the median in the histogram involves summing up the bins of the histogram, the bin where this sum reaches is the median. Updating the histogram as we shift the kernel by one pixel costs operations, and finding the median is a fixed number of operations. Thus, for these images, the median filter has a complexity of , much better than the naive implementation.

Note that this algorithm works for kernels of any shape; is then the number of pixels that exit and enter the kernel when shifting it by one pixel. For a compact 2D kernel this is the height of the kernel, for a non-compact kernel this can be much larger. In 3D it is the height times the depth of the kernel (for example, for a cubic kernel, the complexity is for the naive algorithm, and for the histogram-based algorithm).

This algorithm is due to T.S. Huang and colleagues [1].

But even for 16-bit images, a histogram becomes unwieldy, because finding the median now is not additions on average, but . The constant cost becomes significant compared to the linear cost for reasonable values of .

It has been proposed to augment the 16-bit histogram with smaller histograms with wider bins. For example, each subsequent scale combining 16 bins into one. Updating such a multi-scale histogram is a bit more expensive, but finding the median becomes much cheaper. Still, this does not allow for an algorithm that can handle floating-point images efficiently.

Binary tree algorithm

The histogram here was used as a data structure that makes it easy to compute the median of a set of values, and allows this set to be updated (removing and adding values). A binary search tree can perform the same function but does not rely on values being small integers. A binary search tree is a binary tree where each node contains a value, and the nodes are sorted such that a node’s left child (and all of its descendants) has a smaller value than the node, and the node’s right child has a larger value. Inserting a new value into the tree takes , and so does removing a value. But computing the median still requires to access half the nodes in order, which takes .

An order statistic tree is a binary search tree where each node additionally records its size, which is given by the number of nodes in the subtree rooted at that node. That is, a node’s size is the sum of the sizes of the two children plus one. Armed with this additional information, finding the median (or the node at any given index) takes only . It is no longer necessary to traverse all nodes in order from the lowest value to the given index. The node’s size allows the algorithm to skip most nodes along that path.

So, again assuming a square kernel, we have values in the tree, and for each pixel we need to remove values, insert values, then find the median. This has a complexity of

The complexity analysis here assumes that the binary tree is balanced. Values in an image are locally correlated, meaning that the tree is likely to become unbalanced quickly unless we specifically rebalance the tree when needed. Binary trees typically store some additional value to enable this balancing act (e.g. red-black trees). One form of self-balancing tree is the weight-balanced tree, which keeps the weight of the two subtrees within some factor of each other. Each node stores the weight of the subtree rooted at that node. The weight is defined as one plus the size of the subtree, and we’re already storing the size to compute the order statistic. This means that we can keep the order statistic tree balanced without any additional information or bookkeeping. I followed Hirai and Yamamoto [2] to implement the balancing scheme, using their proposed (3,2) factors: the weight of the two subtrees are kept within a factor of 3 from each other, and the 2 is used when the balance is broken, to decide on whether to do a single or a double rotation at the node to restore balance.

Because pixel values are locally correlated, it is likely that there are repeated values in a neighborhood. A simple modification to the order statistic tree gives it a speed boost when this happens: repeated values are stored in the same node, which now additionally stores this count. This change means there are fewer nodes to traverse when inserting or removing values, or when indexing, and so the computational cost is reduced.

This implementation is in DIPlib, here. It will be available in the next release (whichever comes after the current 3.3.0 release), or you can build it yourself.

The binary search tree is a bit more expensive than the naive algorithm for small kernels. I ran a small experiment to find out how to decide which of the two algorithms to use for any particular call to the dip::MedianFilter() function. Using a rectangular kernel, I varied the width and height independently, from 3 to 39, and determined the running time on some sufficiently large image. This is the result (blue is the naive algorithm, yellow the new order statistic tree algorithm):

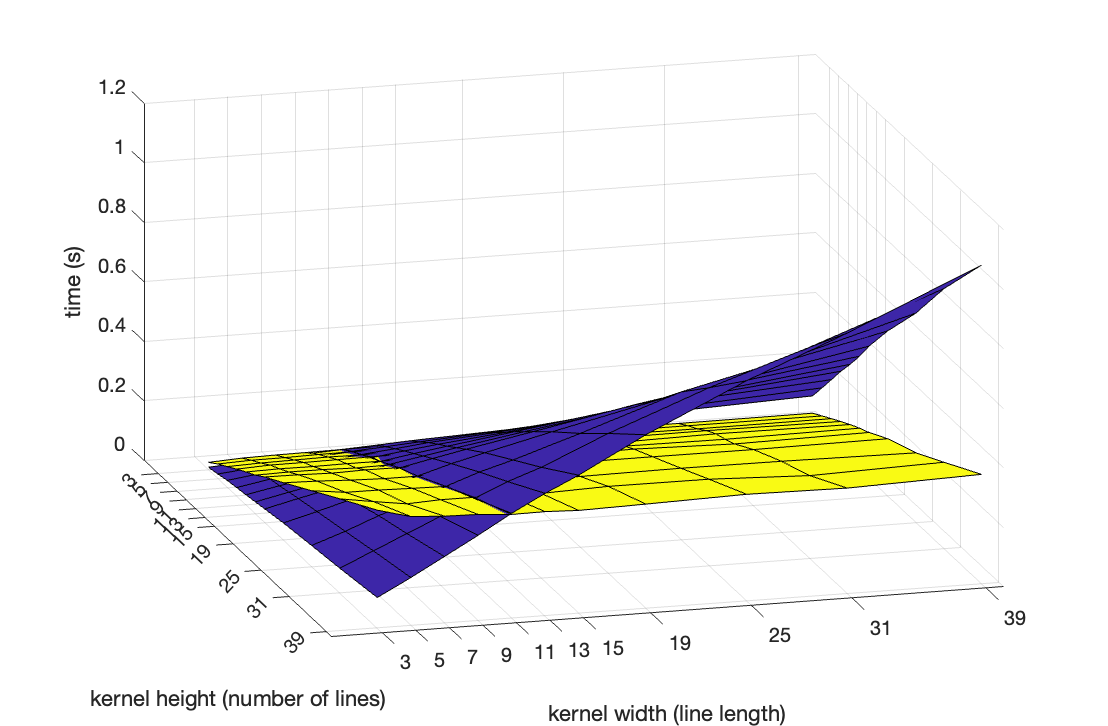
It can clearly be seen that the naive implementation has a running time that is linear in both the width () and the height () of the kernel (). In contrast, the binary tree implementation has a running time that is independent of the width, and linear in the height (). It is actually , but the range is too small to discern the difference.

It can also clearly be seen that the two implementations take the same time for equal to 11. This threshold is likely different on different computers, but I hard-coded this threshold into the dip::MedianFilter() function anyway as it should give some meaningful algorithm selection on any machine.

O(1) algorithm

Perreault and Hérbert [3] figured out how to compute a median filter in constant time. This algorithm is based on Huang’s histogram algorithm, but they store a histogram for each image column, updating these when moving the kernel by one pixel only requires removing one value and adding one value to one of these histograms, then subtracting one histogram and adding another histogram to the main histogram that covers all values under the kernel. OpenCV implements this algorithm, which only works for 8-bit images and square kernels.

Perreault and Hérbert’s paper discusses extension to octagonal kernels (as an approximation to round kernels), which require more intermediate memory (more histograms stored). They claim that for these kernels the algorithm is still , but the increased cost would make this algorithm impractical for all but the largest of kernels.

This algorithm is incredibly fast for any kernel size, as long as the kernel is square and the image is 8-bit. This lack of generality makes it uninteresting to include in DIPlib, which quickly switches to single-precision floating point pixels to avoid rounding errors, and which uses isotropic (round) kernels by default everywhere.

Timing comparisons

The graph below shows the computational time for a square median filter. The new DIPlib implementation is in blue, the constant-time OpenCV implementation is in red, and scikit-image’s implementation (which actually calls SciPy ndimage’s implementation) in green.

For each implementation, I used a single-precision floating-point image (continuous line), an 8-bit unsigned integer version of the same image (dashed line), and that same image divided by 25, meaning that it only has integer values in the range 0-10 (dotted line). This latter case should have many more repeated values within the kernel than the other cases.

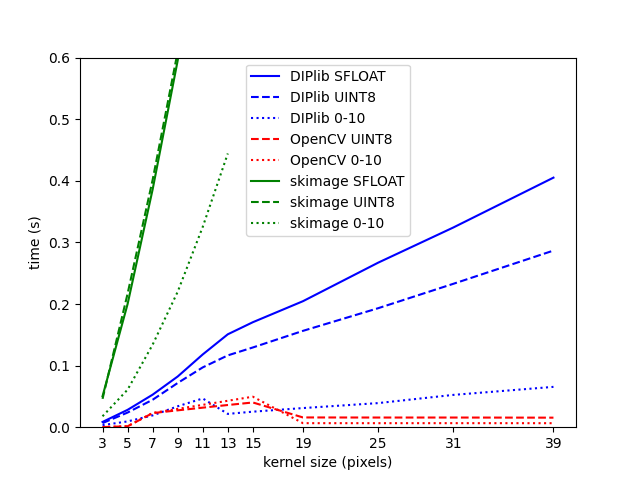
One can see the kink in the blue lines for DIPlib between 11 and 13 pixels, where a different algorithm is chosen. To the left, the curve is quadratic (), to the right it is . Scikit-image’s lines are quadratic, the difference with DIPlib’s line is partially due to quality of implementation, but mostly because DIPlib uses all cores whereas scikit-image is single-threaded. For both implementations, reducing the number of values in the input image strongly reduces the computational cost (dotted lines). Quickselect is faster when many values are identical, and our binary tree implementation has strongly reduced number of nodes when each node represents many pixels with the same value.

The constant-time implementation in OpenCV is not actually constant time. It seems that a different algorithm is used for kernels up to 15 pixels, the constant-time algorithm kicks in at 19 pixels. It also looks like the selection of which algorithm to use was tuned on a machine with different characteristics to mine, meaning that a different algorithm was chosen for some sizes where the constant-time implementation would be more efficient. Because of this, the filter is significantly slower for a kernel of size 15 than for a kernel of size 19.

We can see the same issue in the DIPlib implementation for the dotted line, where the binary tree implementation is faster than what I measured earlier because of the reduced number of different values in the image. Picking the most efficient algorithm under all circumstances is an unattainable dream, I am willing to live with small imperfections like this.