Cris’ Image Analysis Blog

OpenCV is undoubtedly the most popular library for image processing and computer vision. According to its website,

OpenCV is a highly optimized library with focus on real-time applications.

That is, it is built to do real-time computer vision, not precise measurement. This means that OpenCV prioritizes speed over precision. There are many applications where this is the right choice. But there are applications where it isn’t: in my line of work, precision is important.

Over the years I have collected links to questions on Stack Overflow that were prompted by OpenCV’s lack of precision. In today’s blog post I wanted to revisit some of these unexpected results and their cause. This is not meant as an OpenCV-bashing post (though I do enjoy a good bashing now and again), but rather an exploration of the limitations of OpenCV, and maybe a demonstration of why a library like DIPlib has a place in a world dominated by OpenCV.

What I am criticizing here is people trying to use OpenCV for applications where a library such as DIPlib would be a more appropriate choice. If you need precise results or accurate measurements use DIPlib, not OpenCV.

Rounding in interpolation

In this answer, Andras Deak shows how OpenCV’s interpolation output is quantized. It looks like they use fixed-point arithmetic, with a precision of 1/32. I don’t doubt this speeds up computations, but it did produce unexpected results at least once.

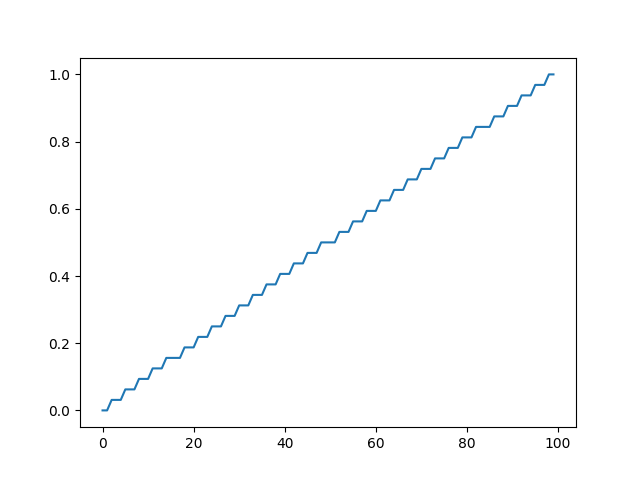
This reproduces the findings. It applies linear interpolation to an image with some pixels set to 0 and some pixels set to 1. It generates 100 new samples in between the last 0 pixel and its neighboring 1 pixel. One would expect the result to be a ramp, a straight line going from 0 to 1. Instead, we see a staircases with 33 steps. Each step is exactly 1/32 high.

import numpy as np
import cv2
import matplotlib.pyplot as plt

input = np.zeros((1, 100), dtype=np.float32)
input[:, 50:] = 1

grid_x = np.linspace(49, 50, 100, dtype=np.float32)[None, :]
grid_y = np.zeros(grid_x.shape, dtype=np.float32)
output = cv2.remap(input, grid_x, grid_y, interpolation=cv2.INTER_LINEAR)

plt.plot(output[0, :], '-')
plt.show()

Color space conversion is lossy

This question is from someone surprised at the round trip RGB (or rather BGR, why reverse the order?) to HSV and then back to RGB causes visible color banding.

import cv2
import numpy as np
import matplotlib.pyplot as plt

x = np.arange(256)
x, y = np.meshgrid(x, x)
z = np.zeros(x.shape)
img = np.stack((x / 3 + 165, y / 3 + 100, z), axis=2)
img = img.astype(np.uint8)

imghsv = cv2.cvtColor(img, cv2.COLOR_BGR2HSV)
imgback = cv2.cvtColor(imghsv, cv2.COLOR_HSV2BGR)

_, ax = plt.subplots(1, 2)
ax[0].imshow(img)
ax[1].imshow(imgback)
plt.show()

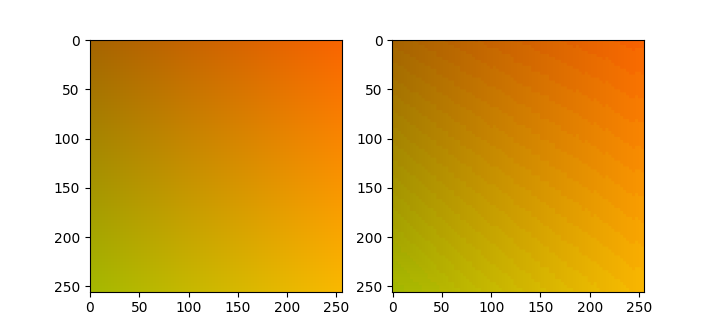
The problem is caused by rounding, which apparently happens mostly in the hue channel. OpenCV rounds the 360 degrees of hue to 180 integer values, meaning that 30% of the dynamic range on the hue channel is not used. That said, I’m not sure if mapping the 360 degrees to all 256 values of the 8-bit integer would be sufficient to make the round trip not introduce visible artifacts. DIPlib outputs floating-point images after color conversion by default, as does scikit-image. Using floating-point images is the only way to guarantee a lossless roundtrip.

Perimeter measurement is biased and imprecise

The more problematic precision issues are the ones where it is not done on purpose to save time. For example, OpenCV’s object perimeter measurement is imprecise and biased, even though computing it properly is not a significantly more expensive. I wrote about computing the perimeter many years ago. OpenCV measures the length of the polygon that goes through each boundary pixel. This measurement is correct only for axis-aligned rectangles and rectangles rotated by 45 degrees. It overestimates the length of any other perimeter.

This experiment computes the perimeter of a square at many orientations, averaging over different sub-pixel shifts to get a better estimate of the average measurement error:

import cv2
import diplib as dip
import numpy as np
import matplotlib.pyplot as plt

R = 80
N = 16
angles = np.linspace(0, np.pi / 2, 41)
perimeter = []
xx = dip.CreateXCoordinate((256, 256))
yy = dip.CreateYCoordinate((256, 256))
rng = np.random.default_rng()
for phi in angles:
    cv_perimeter = 0
    dip_perimeter = 0
    for jj in range(N):
        offset = rng.random(2)
        x = (xx + offset[0]) * np.cos(phi) - (yy + offset[1]) * np.sin(phi)
        y = (xx + offset[0]) * np.sin(phi) + (yy + offset[1]) * np.cos(phi)
        img = (dip.Abs(x) <= R) & (dip.Abs(y) <= R)
        arr = np.asarray(img, dtype=np.uint8)
        cnt, _ = cv2.findContours(arr, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)
        cv_perimeter += cv2.arcLength(cnt[0], True)
        msr = dip.MeasurementTool.Measure(+img, features=['Perimeter'])
        dip_perimeter += msr[1]['Perimeter'][0]
    perimeter.append((cv_perimeter / N, dip_perimeter / N))

plt.plot(angles, perimeter)
plt.plot([0, np.pi / 2], [8 * (R - 0.5), 8 * (R - 0.5)], 'k:')
plt.xlim((0, np.pi / 2))
plt.xticks(np.linspace(0, np.pi / 2, 5), ['0', 'π/8', 'π/4', '3π/4', 'π/2'])
plt.legend(['OpenCV', 'DIPlib'])
plt.xlabel('angle')
plt.ylabel('estimated perimeter')
plt.title('Perimeter of rotated square')
plt.show()

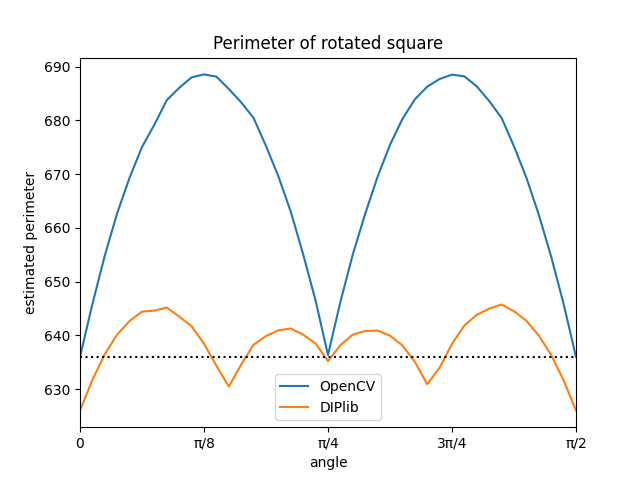
As I mentioned earlier, OpenCV gets it exactly right for 0 and 45 degree angles, and overestimates the perimeter for all other angles. In contrast, the corner counting method used by DIPlib is unbiased (averaged over all angles, it gets the right value), and the maximum error is much smaller than for the naive method.

The poor perimeter estimate recently stumped two people, posting questions on Stack Overflow about it less than a week apart (#1, #2). Both were trying to compute the circularity measure, (with the area and the perimeter). This is supposed to be 1 for a circle, and smaller for other shapes. But because OpenCV overestimates the perimeter of the circle, this measure never reaches 1 (except for very small circles, where it severely underestimates the perimeter).

This experiment draws circles of different radii, with different sub-pixel shifts, and measures their perimeter using OpenCV and DIPlib:

import cv2
import diplib as dip
import numpy as np
import matplotlib.pyplot as plt

radii = [2, 3, 5, 10, 20, 30, 50, 100, 200]
sz = 10 + 2 * radii[-1]
error = []
N = 16
xx = dip.CreateXCoordinate((sz, sz))
yy = dip.CreateYCoordinate((sz, sz))
rng = np.random.default_rng()
for R in radii:
    cv_perimeter = 0
    dip_perimeter = 0
    for jj in range(N):
        offset = rng.random(2)
        img = ( (xx + offset[0])**2 + (yy + offset[1])**2 ) < R**2
        arr = np.asarray(img, dtype=np.uint8)
        cnt, _ = cv2.findContours(arr, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)
        cv_perimeter += cv2.arcLength(cnt[0], True)
        msr = dip.MeasurementTool.Measure(+img, features=['Perimeter'])
        dip_perimeter += msr[1]['Perimeter'][0]
    true_perimeter = 2 * np.pi * R
    error.append((cv_perimeter / N / true_perimeter, dip_perimeter / N / true_perimeter))

plt.plot(radii, error)
plt.plot([2, 200], [1, 1], 'k:')
plt.xscale('log')
plt.legend(['OpenCV', 'DIPlib'])
plt.xlabel('radius (px)')
plt.ylabel('measured perimeter as fraction of true perimeter')
plt.title('Error in circle perimeter measurement')
plt.show()

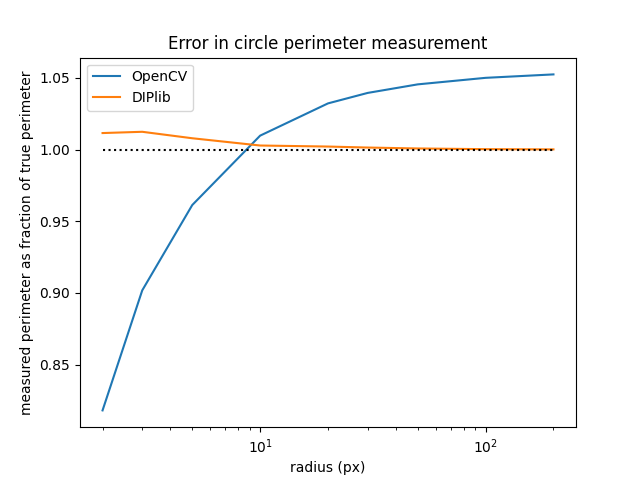
This shows that OpenCV tends to overestimate the circle perimeter by a factor of 6% for larger circles, whereas the unbiased estimator that DIPlib uses tends towards the right value for larger circles. For very small circles OpenCV underestimates the perimeter. This is because it measures the length of the polygon formed by the centers of the border pixels of the object. This polygon is slightly smaller than the object itself, as it doesn’t go around all the object pixels, it goes through the outermost pixels of the object. For circles this introduces a bias in the perimeter length of (the radius is 0.5 pixels too small, and is ). This bias is small in comparison to the bias due to the length overestimation for larger circles, but for very small circles it dominates.

Non-symmetric circular structuring elements

My PhD thesis was about using morphological openings and closings to measure grain sizes, using what is called a granulometry. If I had used OpenCV for my thesis, I would have had to roll my own circular structuring elements. Because OpenCV’s are not circularly symmetric. If you create any circular structuring element, then rotate it 90 degrees (or equivalently, transpose the array), then you get a different shape:

import cv2
import numpy as np
import matplotlib.pyplot as plt

kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (45, 45))
comparison = np.dstack((kernel, kernel.transpose(), kernel.transpose())) * 255
plt.imshow(comparison)
plt.show()

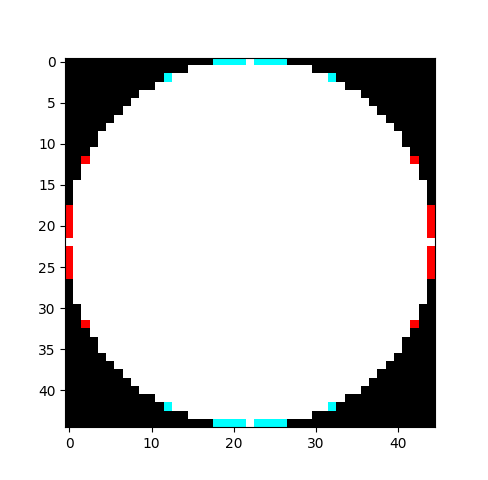
The white and red parts together is the generated kernel, the transposed kernel is the white and cyan parts.

This has already been filed as a bug. And as I’ve said before, we shouldn’t fault a large, complex library like OpenCV for having bugs. But that this type of bug exists does illustrate that the library’s focus is not on precise results; if it were, this bug would never have gotten though testing.

Non-idempotent morphological opening

Another strange issue with the morphological opening and closing is shown in this question. The image boundary is not treated correctly, causing repeated applications of the same filter to continue affecting the image. The opening and closing are supposed to be idempotent, meaning that applying the same filter multiple times in sequence should have the same effect as applying it only once.

I wouldn’t fault anyone for a bug, what prompts me to include it here is that this was reported as a bug, but the ticket was dismissed as a “question or other no-action item”, which I interpret as nobody being interested in fixing it. This is an issue that matters in many cases, but none of those cases are intended use cases of OpenCV. Typical users of OpenCV wouldn’t care about the difference.

One point of criticism

All of that wasn’t criticism, OpenCV developers made choices favouring speed over precision. Those choices obviously will produce surprises if one wants to use OpenCV for applications that require precision. You just need to use the right tool for the job!

However, given that OpenCV is designed around speed, it is indeed very strange that it doesn’t always implement the fastest known algorithms.

Take for example the Gaussian filter, arguably the most important basic filter in any image processing toolbox. This experiment times the computation of the Gaussian filter with a sigma of 5 along both axes, repeated 1000 times. Both libraries implement the filter quite similarly: They compute the kernel size differently based on the sigma parameter, but in this case they both produce a Gaussian kernel with 31 samples along each axis. Both libraries compute the Gaussian as a separable filter, as one would expect.

import numpy as np
import diplib as dip
import cv2
import timeit

rng = np.random.default_rng()
img = rng.integers(256, size=(1024, 1280)).astype(np.float32)

print(timeit.timeit(
    lambda: cv2.GaussianBlur(img, ksize=(0, 0), sigmaX=5),
    number=1000))
print(timeit.timeit(
    lambda: dip.Gauss(img, sigmas=5),
    number=1000))

On my machine, DIPlib’s filter is about twice as fast (6.87 s for OpenCV, 3.17 s for DIPlib).

As I understand it, OpenCV does not use the symmetry of the 1D Gaussian kernel when computing the convolution. For a general 1D kernel with samples, applied to an image line at , we compute

But if we know that is symmetric, with and so on, then we can instead compute (assuming is odd)

saving us multiplications. If OpenCV is serious about speed, this seems an obvious optimization to make. DIPlib has a dedicated convolution also for 1D antisymmetric kernels, such as the first and third derivatives of the Gaussian.

Likewise, OpenCV’s dilation, the most basic morphological operator, is the naive algorithm, although implemented very efficiently. The naive algorithm computes the maximum over the pixels under the kernel, shifts the kernel, computes the maximum over the new set of pixels, etc. It does not attempt to use the result for the previous pixel to make the current pixel’s computation lighter. OpenCV does recognize that the square kernel is separable, and so has an implementation that is linear in the length of the side of the square. A circular kernel is not separable, which means that the naive algorithm is quadratic in the circle’s diameter (it scales with the area).

Here’s an experiment:

import numpy as np
import diplib as dip
import cv2
import timeit
import matplotlib.pyplot as plt

rng = np.random.default_rng()
img = rng.integers(256, size=(1024, 1280)).astype(np.float32)

times = []
sizes = [7, 15, 31, 63, 127]
for size in sizes:
    kernel = cv2.getStructuringElement(cv2.MORPH_RECT, ksize=(size, size))
    t1 = timeit.timeit(
        lambda: cv2.dilate(img, kernel, iterations=1),
        number=1000) / 1000
    t2 = timeit.timeit(
        lambda: dip.Dilation(img, dip.SE(size, "rectangular")),
        number=1000) / 1000
    kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, ksize=(size, size))
    t3 = timeit.timeit(
        lambda: cv2.dilate(img, kernel, iterations=1),
        number=100) / 100
    t4 = timeit.timeit(
        lambda: dip.Dilation(img, dip.SE(size, "elliptic")),
        number=100) / 100
    times.append((t1, t2, t3, t4))

times = np.array(times)

plt.plot(sizes, times[:,0], ".:r", label="Square, OpenCV")
plt.plot(sizes, times[:,1], ".:b", label="Square, DIPlib")
plt.plot(sizes, times[:,2], ".-r", label="Circle, OpenCV")
plt.plot(sizes, times[:,3], ".-b", label="Circle, DIPlib")
plt.yscale("log")
plt.xlabel("kernel diameter (pixels)")
plt.ylabel("time for a single dilation (s)")
plt.legend()
plt.show()

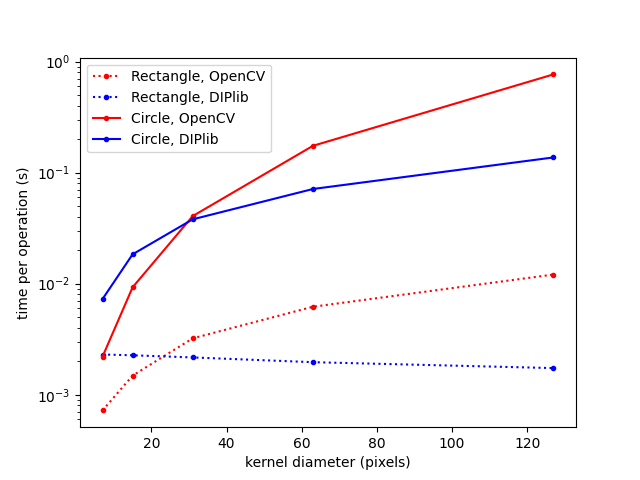
For smaller kernels, OpenCV is much faster than DIPlib. They really put effort into the quality of the implementation. But it is obvious from the graph that DIPlib implements the better algorithms. For both kernel shapes, DIPlib scales better than OpenCV: the square kernel is independent of the size, and the circular kernel scales with the diameter (not the area). I have written before about optimizing the wrong algorithm, MATLAB has a similar issue.

By the way, the reason that OpenCV can be so much faster than DIPlib for small kernels is because OpenCV’s implementation is explicitly 2D, and requires pixels within an image line to be consecutive in memory. This allows the implementation to optimize memory access patterns. DIPlib prefers more generic algorithms. DIPlib’s implementation works for an arbitrary number of dimensions, with an arbitrary memory layout. There are some optimizations that are just not possible without those additional constraints.