Cris’ Image Analysis Blog

Last year I wrote about computing the the boundary length and various other measures, given an object’s chain code. The chain code is a simple way of encoding the polygon that represents a 2D object. It is very simple to compute the object’s convex hull given this polygon. Why would I want to do that? Well, the convex hull gives several interesting object properties, such as the convexity (object area divided by convex hull area). Certain other properties, such as the Feret diameters, are identical for an object and its convex hull, and the convex hull thus gives an efficient algorithm to compute these properties.

Avraham Melkman (1987) has published a very efficient algorithm to compute the convex hull given a polygon (find the PDF through Google Scholar). It has been said that this might very well be the most efficient algorithm possible. It visits each polygon vertex only once, and keeps only those vertices that form the convex hull. To accomplish this, it uses a deque (also known as double-ended queue) to represent the convex hull. The deque has 4 basic operations: push and pop add and remove elements from the end of the queue, and insert and remove add and remove elements from the front of the queue. By using such a data structure, Melkman was able to add and remove vertices from his convex polygon at either side. The points in the deque always constitute a convex polygon, and is the convex hull of the input points seen up to that point.

The Melkman algorithm also depends on a function, which I’ve called position here, which returns 1 if pt3 is to the right of the directed line formed by pt1 and pt2, -1 if it is to the left, or 0 if all three points are collinear (form a straight line). This function simply returns the sign of the signed area of the parallelogram given by the vectors pt2-pt1 and pt3-pt1. It we embed these vectors in 3D (adding the value 0 as the z component), and compute the cross product, the norm of this cross product gives the area of the parallelogram, whereas its direction is given by the ordering of the three points on the plane (as per the right-hand rule). The cross product will, however, always have x and y components equal to 0, so we only need to compute the z component. Let’s define an anonymous function position(pt1,pt2,pt3) for this:

position = @(pt1,pt2,pt3) ...
   sign( (pt2(1)-pt1(1))*(pt3(2)-pt1(2)) - ...
         (pt2(2)-pt1(2))*(pt3(1)-pt1(1)) );

Before we can apply the algorithm, we’ll need some data. I like the image “cermet”. Let’s pick object #31, and get its chain code:

img = label(readim('cermet')<120);
cc = dip_imagechaincode(img,2,31);  % for DIPimage 2
% cc = traceobjects(img,31,2,'chain code')  % for DIPimage 3, use cc{1} instead of cc.chain below

The code below, however, takes a polygon represented by a set of points, not a chain code. We can easily convert the chain code cc into a list of coordinates coords (this is the same code as in the post on chain codes):

directions = [ 1, 0
               1,-1
               0,-1
              -1,-1
              -1, 0
              -1, 1
               0, 1
               1, 1];
coords = cumsum(directions(cc.chain+1,:));
N = size(coords,1);
% Draw input polygon:
figure('position',[1000,500,450,450]);
plot([coords(:,1);coords(1,1)],[coords(:,2);coords(1,2)],'b-')
hold on, axis equal, axis off

Melkman’s algorithm starts by taking the first three points in the list and forming them into a start of the convex hull. However, the algorithm assumes these points are not collinear. So let’s examine the first 3 points in the set, and delete the second one if all 3 are collinear:

while N>=3 && position(coords(1,:),coords(2,:),coords(3,:)) == 0
   coords(2,:) = [];
   N = size(coords,1);
end

At this point, we’d of course check to make sure that we have more than 3 points left. If not, we’re done! There is also a special case that could happen if our object is a single line. In this case, all points in the object are collinear, and the code above leaves only 2 points. We’d need to detect this case, and make sure that we keep the two extreme points, rather than the first and last points in the list. Otherwise, length measurements on our convex hull will be wrong.

We start by creating a deque data structure D (in MATLAB we can just use a simple array), and put the first three points in it. We first check the order of these points, and put them in the deque so that the polygon is right-turning. Furthermore, we always want the first and last point in our deque to be the same point:

if position(coords(1,:),coords(2,:),coords(3,:)) > 0
   D = coords([3,1,2,3],:);
else
   D = coords([3,2,1,3],:);
end
% Add convex hull to figure:
h = plot(D(:,1),D(:,2),'ro-');

Next, the algorithm takes one new point v at the time, and checks where it lies with respect to the first two points and the last two points in the deque. This tells us if the point is already inside the convex hull or not. If it is inside, we ignore the point and take the next one. If it is not inside, we’ll be wanting to add this point at the beginning and at the end of the deque (push and insert). But before we add this new point, we need to remove (pop and remove) previous points that will potentially end up inside the convex hull. We start with the end of the deque, and see if the last point is inside the line formed by the second to last point and the new one. If so, we pop that point. This is repeated until we cannot pop the last point any more, and then push the new point. We repeat the same procedure with the front of the deque, removing points and then inserting the new one. Now the algorithm loops back to process the next point. This is the code:

ii = 3;
while 1
   ii = ii+1; if ii>N, break, end
   v = coords(ii,:);
   while position(v,D(1,:),D(2,:)) >= 0 && ...
         position(D(end-1,:),D(end,:),v) >= 0
      ii = ii+1; if ii>N, break, end
      v = coords(ii,:);
   end
   if ii>N,break,end
   while position(D(end-1,:),D(end,:),v) <= 0
      D(end,:) = []; % pop
   end
   D = [D;v];        % push v
   while position(v,D(1,:),D(2,:)) <= 0
      D(1,:) = [];   % remove
   end
   D = [v;D];        % insert v
   % Update convex hull in figure:
   set(h,'xdata',D(:,1),'ydata',D(:,2));
   pause(0.2)
end
D(end,:) = []; % start and end points are the same, remove one.

When running the code, you will see the convex hull being updated as new points are examined by the algorithm (note that the slowness comes from the pause statement in the code!). At the end of the algorithm you’ll see this on your screen:

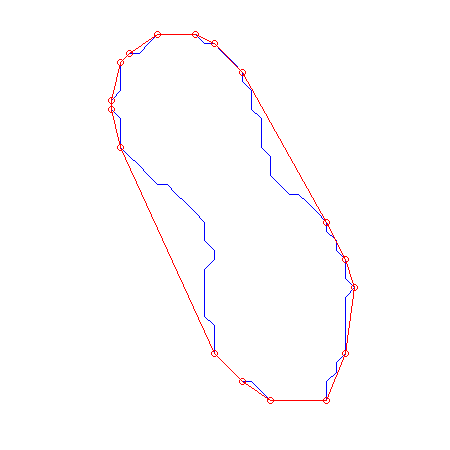
In a future post we’ll use this convex hull to compute Feret diameters.